
Here you can roll out your very own repeating border pattern—a frieze. You see such patterns in tire tracks, on belts, ribbons, and lace, patterns that frame doors, pictures, pottery, and baskets. How you place the sponges on the roller will determine the symmetry of your pattern.
Can you make a pattern that looks like footprints of someone walking on a beach? Walking on a tightrope? Hopping on one foot? Hopping with both feet? Can you make a pattern that looks like a row of Christmas trees? A pattern that zig-zags up and down?
The frieze patterns in the picture were inspired by South African bead patterns and use repeated copies of a single striped rectangle and its mirror image.

Your decorated roller repeats the decoration every time the roller makes a full turn. This creates a periodic frieze pattern. If you shift (translate) the pattern backwards or forwards you can superimpose the pattern exactly on itself, and it will look as though no motion has taken place. The smallest such shift is called the period of the pattern, and we say the pattern has translation symmetry.
In this frieze pattern of ducks, two facing ducks were placed on the roller. The red line is equal to the circumference of the roller, and its length is the period of the pattern.

Periodic frieze patterns can have other symmetries. Any motion that, when applied to the pattern, makes the pattern coincide with itself so that it looks as though no motion at all has happened, is called a symmetry of the pattern.
If this duck pattern is flipped around the blue line, the duck images will coincide. The vertical line acts as a mirror, reflecting ducks on one side of the mirror onto ducks on the other side of the mirror. This pattern has vertical reflection symmetry
Imagine this pattern is repeated forever in both directions. What other vertical lines can act as mirrors to reflect the pattern onto itself?
Use a different shape to make a pattern with vertical reflection symmetry.

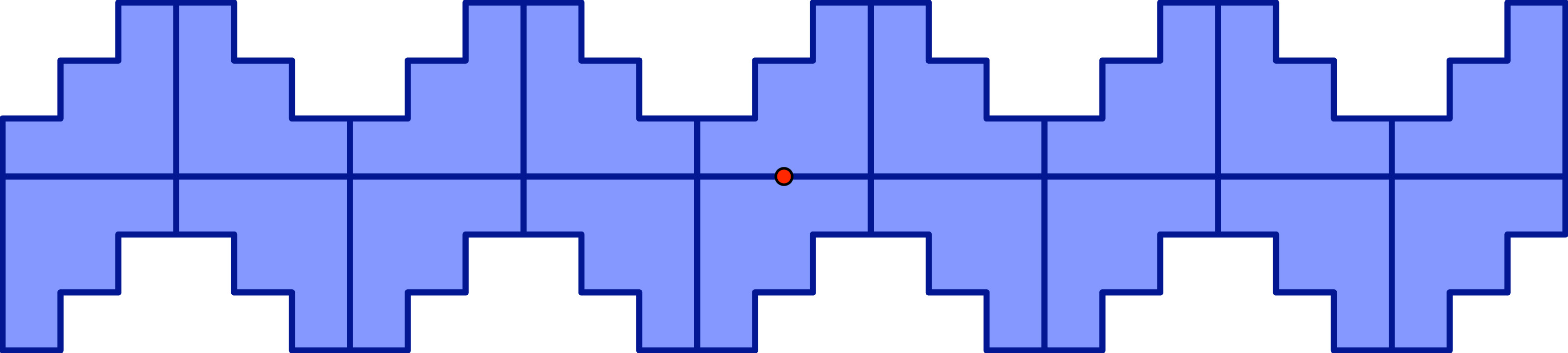
You can half-turn a frieze pattern, that is, turn (rotate) it 180o about a point at the middle of the strip. If the rotated pattern coincides with the original pattern, we say the pattern has half-turn symmetry, or 2-fold rotation symmetry.
Rotating this pattern 180o about the red point turns the pattern upside down, yet the pattern looks like it has not moved. The red point is called a rotation center, and the pattern has half-turn symmetry.
Imagine this pattern is repeated forever in both directions. What other points can act as rotation centers?
Can you make a pattern with half-turn symmetry using a different shape? Does your pattern look the same upside down?

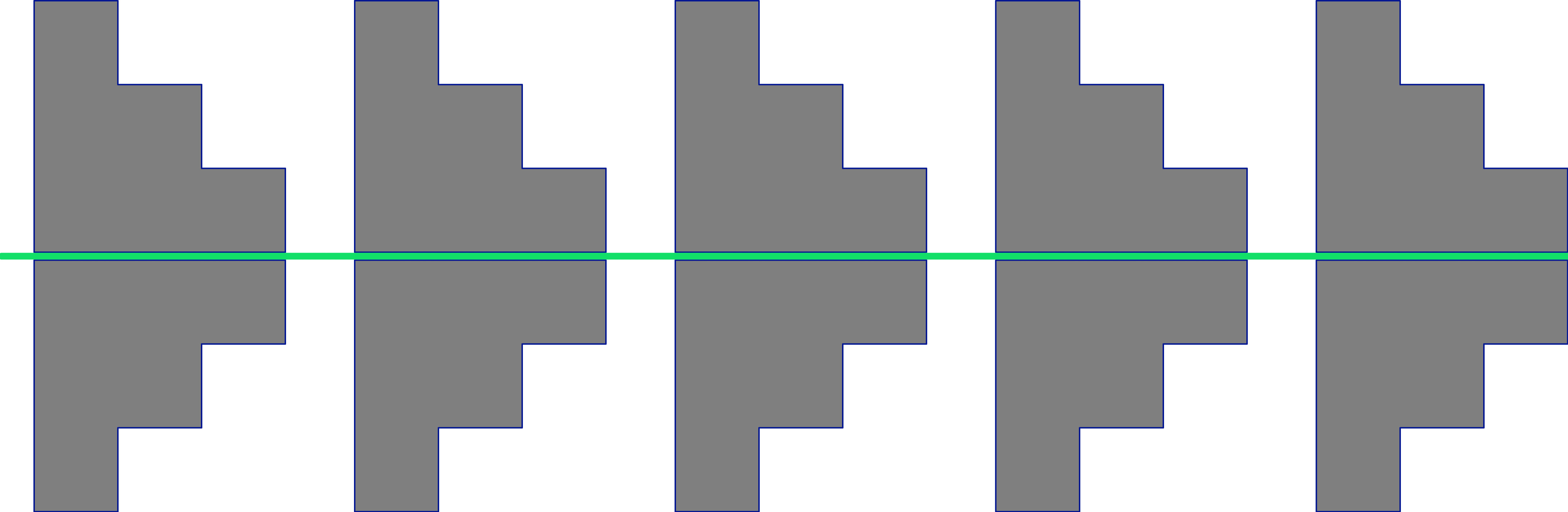
You can fold a frieze pattern along its center line so that the top and bottom edges of the strip match. If the top and bottom halves of the pattern match, we say the pattern has horizontal reflection symmetry. The fold line acts like a mirror, reflecting the top and bottom halves of the pattern onto each other.
Here is a frieze pattern made with the step shapes. The pattern has horizontal reflection symmetry. The green line is the center line of the pattern, and acts like a mirror.
Can you make a frieze pattern with horizontal reflection symmetry using a different shape?
You can move a frieze pattern by sliding it and then immediately reflecting it across the center line of the strip—this combined motion is called a glide-reflection. If, after this combined motion, the pattern looks like it hasn’t moved, we say the pattern has glide-reflection symmetry. The footprint pattern made by someone who is walking along a straight path will have glide-reflection symmetry.
Here is a pattern with glide-reflection symmetry. Imagine it continues forever. Gliding the pattern the length of the red line and then immediately flipping it over the horizontal green line, each duck will land exactly on another duck.
Can you make a pattern with glide-reflection symmetry?

Challenge: Make a water frieze pattern with at least two symmetries in addition to translation symmetry.
A dark frieze pattern against a light background usually creates two different patterns. There is a dark pattern against a light background, and a light pattern against a dark background. But for some frieze patterns the light and the dark patterns are the same! A pattern of equally spaced black bars like this is an example:
| | | | | | | | | | | | | | | | |.
Here is a more complex and beautiful example. Not only is the white background pattern the same as the black pattern, but a halfturn about the red dot interchanges the black and the white patterns!
Challenge: Use the triangle or the step shapes to make a water frieze pattern in which the background and the printed pattern are exactly the same pattern.

A periodic frieze pattern must have translation symmetry, but may have in addition one or more of these: 2-fold rotation symmetry, horizontal reflection symmetry, vertical reflection symmetry, glide-reflection symmetry. Although there are infinite design possibilities for frieze patterns, they can be sorted into exactly seven classes (types) according to their symmetries. Mathematicians have given each type a short 2-symbol name.
Can you identify the symmetries of these seven patterns (each represents one of the seven types.) Hint: The first pattern has only translation symmetry, the next four patterns have one additional symmetry, the next to last has three additional symmetries, and the last has four additional symmetries.

With paper and scissors you can produce a frieze pattern having vertical reflection symmetry. Take a long strip of paper and accordion-fold it so the folds are perpendicular to the edges of the strip. Then cut out a half-shape, taking care to leave some parts of the folds uncut. The fold lines act as mirror lines. “Paper doll” frieze patterns can be created this way.
If you take your accordion-folded paper and fold it in half over the center line of the strip, you can cut it to make a frieze pattern that has vertical and horizontal reflection symmetry.


The role of symmetry (as showcased in these frieze patterns) was brought to the forefront of modern science by German mathematician Emmy Noether. After expulsion from Gottingen, she made a new home in Bryn Mawr, Pennsylvania, where she continued her foundational research, studying symmetry both in mathematical realms like algebra, and in the physics of conservation laws.
The Desai Family provided support that made Water Frieze possible.
Most tractor tires have a tread design that rolls out a frieze pattern with glide-reflection symmetry. What might be a reason for this choice of tire tread design?

Frieze patterns have been found in almost every culture and period of history. Decorative art seems to be a human need, a way to express identity or beliefs, and to make plain functional items beautiful. Some of the oldest rollers with carved patterns that could make frieze patterns (seals) in wet clay date to the period between 3100 BCE and 2900 BCE — 5,000 years ago!
Periodic frieze patterns can be found in tiled walls and floors of ancient Greece and Rome, in decorated pottery, carvings, baskets and beadwork of native peoples of the Americas, Africa and Asia. Patterns with particular motifs and particular symmetry can be used by archeologists as a marker (identifier) for a culture that may have disappeared hundreds of years ago. The book “Symmetries of Culture” by Dorothy Washburn and Donald Crowe explains how to analyze patterns by their symmetry and how that analysis can be a useful tool for archeologists.

Although the frieze patterns you roll out have periodic symmetry, not all patterns or carvings called friezes have this symmetry. In fact, some of the most famous sculpted artworks called friezes are carved in marble on the architraves of ancient Greek temples; these are decorative bands between the top of the exterior columns and the temple roof. Friezes can also wrap around the exterior wall of the cella, an inner chamber of the temple. These friezes usually depict humans and gods in daily life and warfare. The most famous of these friezes was in the Parthenon, completed around 438 BCE.


