
Here you can shape your very own tiles that will tessellate–guaranteed!
Choose one of the twelve polygon tessellations on the nearby screens, then poke and pull on the edges and vertices of one tile to change its shape. As you change the shape of one edge, another edge of the tile will change the same way. The tiles will always fit together in the new tessellation you create. As you change the edge of one tile, copies of these edges on all other tiles will change automatically as well.
Use your imagination to create a shape that suggests an animal or other object. Now add detail to your tile by drawing with the pointer. And finally, when the cutter is running, a MoMath staffer can cut the tiles of your tessellation to take home!
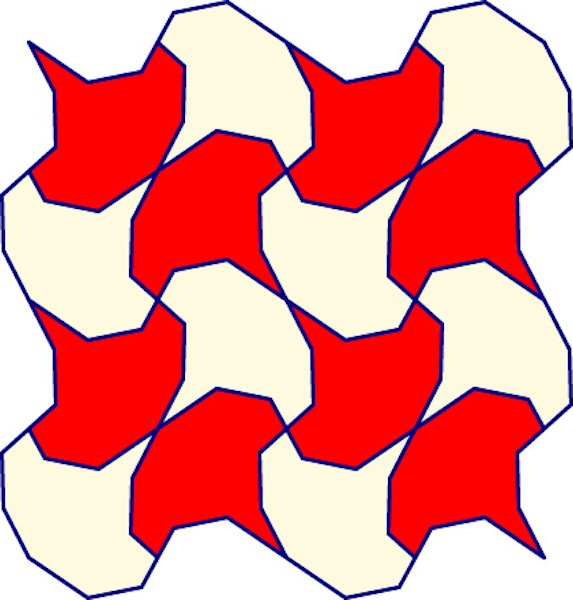
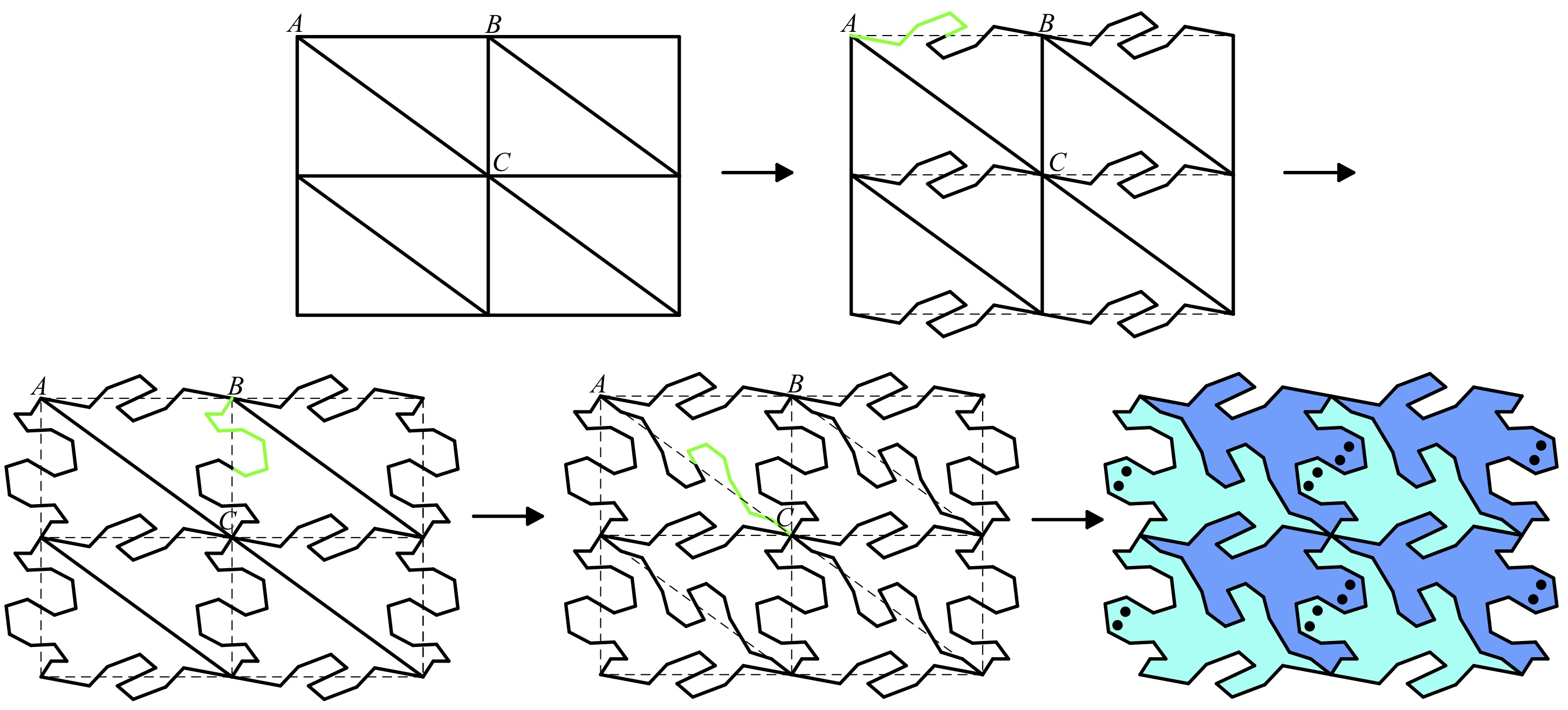
Here is how to form an Escher-like tessellation of lizards. Start with the triangle tessellation in the top row, second from the left.
Each triangle in the beginning tessellation can turn into the triangle next to it by rotating a half-turn (180o) about the midpoint of their shared edge. Push and pull on the left half of edge AB to make a new bumpy (green) edge. Automatically your changes are half-turned about the midpoint of AB to complete the other half of a new edge joining A to B. The program also changes all triangle edges related to AB. Repeat this process for edge BC, making a new bumpy edge from B to the midpoint of edge BC, and then repeat again to complete the tile with a new bumpy edge joining C to A. Finally, add details to complete the tessellation of lizards.
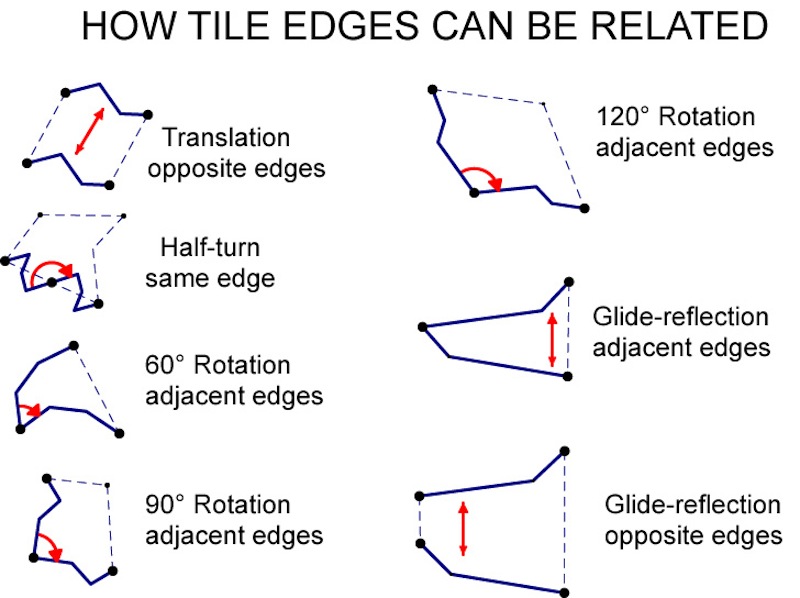
The edges of the tiles in these tessellations are related to each other by rotations (turns), translations (slides), or glide-reflections (slide plus reflection).
1. Translations match opposite edges of a tile.
2. A half-turn (rotation of 180o) about the midpoint of an edge matches half the edge with the other half.
3. Rotations of either 60o, 90o, or 120o about a corner (vertex) match an edge with an adjacent edge.
4. Glide-reflections can match an edge to an adjacent edge or to an opposite edge. In the picture, an edge is translated up or down and then reflected about a vertical line through its middle.
When you change the shape of one edge of a tile, one of these motions changes the matching edge of the tile, and the two new edges are related by the same motion.
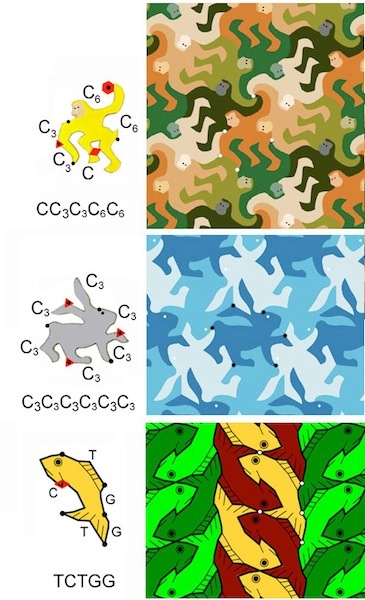
The German mathematician Heinrich Heesch made up a way to label tiles in tessellations like the ones in Tile Factory. Each edge of a tile is assigned a letter (T, C, or G), depending on how the edge is related to another edge of the tile (or to itself). The label also tells how a tile will fit against another tile of the same shape.
The letter T is assigned if an edge is related to its opposite edge by a translation.
The letter C is assigned if an edge can be rotated 1800 about its midpoint and match itself.
The notation C6, C4, or C3 means that a 60o, 90o, or 120o rotation about the edge’s endpoint takes the edge into an adjacent edge.
The letter G is assigned if a glide-reflection takes the edge to an adjacent or opposite edge.
The image shows three tiles with their Heesch labels. The monkey tile has 5 edges, the rabbit tile has 6 edges, and the fish tile has 5 edges. In the pictures, dots identify tile vertices (ends of edges) of one tile, and rotation centers are marked by: diamond = 180o center, triangle = 120o center, hexagon = 60o center.
Find the monkey and rabbit tiles in the exhibit Tessellation Station. As you put together many tiles of the same shape, notice how you are turning the tile to make edges fit together– just like their labels tell us.

American mathematician Marjorie Lee Browne (1914 – 1979) would likely have enjoyed this exhibit on bending and stretching to make tessellating tiles, as they relate to both her research in linear and matrix groups, and her passion for encouraging math education and exploration for all.

Tokyo artist Makoto Nakamura is a graduate of Tara Art University and founder of the Japan Tessellation Design Association (JTDS). Inspired by Escher’s work, Nakamura has made dozens of wonderful tessellations by creatures, including the monkey tile, rabbit tile, and dinosaur tile. And like Escher, he has used his tessellations to create other fanciful worlds in prints and drawings, as well as jigsaw puzzles, layered three-dimensional renditions, and sculpted tessellations on spheres. In his prints, his interlocked creatures metamorphose and break free from their locked positions. On his web site, you can find a large catalog of his tessellations, live animations of his creatures metamorphosing, as well as animated puzzle games.

Dr. Doris Schattschneider is an internationally recognized expert in tessellations of the plane and the work of M.C. Escher. She is the author of M.C. Escher: Visions of Symmetry. Dr. Schattschneider received her PhD from Yale University in 1966 and taught for 34 years on the math faculty at Moravian College, where she is now Professor Emerita of Mathematics.
Professor Schattschneider provided mathematical background for the creation of the tessellating tiles that you can design in Tile Factory.


