The goal of this game is to collect three numbers that add up to 15 before your opponent does.
Think before you choose!
What three numbers from one to nine add to 15?
If you have already selected 1 and 6, what number do you need to win?
If your opponent has selected 2 and 9, what number should you choose next to stop them from winning?
See the following page for the answers to these questions.

Q: What three numbers from one to nine add to 15?
A: There are different correct answers. For instance, 3+4+8=15.
Q: If you have already selected 1 and 6, what number do you need to win?
A: Since 1+6+8=15, you need 8 to win.
Q: If your opponent has selected 2 and 9, what number should you choose next to stop them from winning?
A: Since 2+9+4=15, you should choose 4 to stop your opponent from winning the game.

There are eight different sets of three numbers that add to 15. They are {9,5,1}, {9,4,2}, {8,6,1}, {8,5,2}, {8,4,3}, {7,6,2}, {7,5,3} and {6,5,4}.
We can use these eight sets to form a magic square. A magic square is a table where the numbers in each row, column, and diagonal all sum to the same number — the magic number.
To win Finding Fifteen, you have to be the first player to get all the numbers in a row, column, or diagonal of this magic square.
Do you know any other games where the goal is to claim all the squares in a row, column, or diagonal before your opponent does?


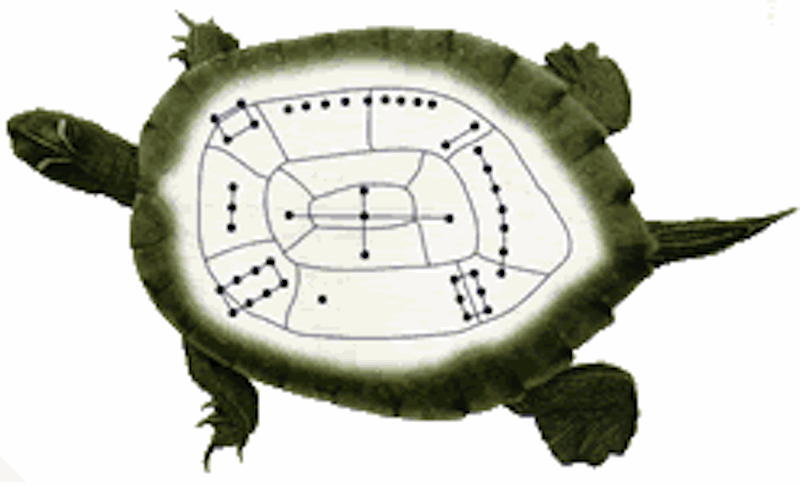
This magic square was found in ruins in China. It is between seven and eight hundred years old!

This is Melencolia I, an engraving created by German painter, printer, and mathematician Albrecht Dürer in 1514. Can you find the magic square?
.jpeg)
Here’s a close-up of the magic square in Melancolia I. Check to see that the rows, columns, and diagonals add to 34. Dürer created this engraving in 1514. Note how the date appears in the magic square!

This is a sculpture in the Eaton Fine Art Gallery in Florida created by artist Patrick Ireland. It’s a magic square, but the numbers in the square are represented in a different way. Can you figure out the nine numbers and verify that it’s a magic square?

This photograph is the work of Russian-born American artists Valeriy Gerlovin and Rimma Gerlovina. Though not on display currently, it was donated to the Art Institute of Chicago in 1991.

National Grid provided support that made Finding Fifteen possible.

John Robert Hendricks was a Canadian mathematician who specialized in magic squares, cubes, and hypercubes. He published over 50 articles and several books on these topics.
John’s interest in magic squares and cubes began when he was 13. He became the first person in the world to successfully make and publish five- and six-dimensional magic hypercubes as well as a variety of inlaid magic squares and cubes.

While many people think of mathematics as an extension of arithmetic, such as knowing your times tables, training in mathematics is actually much more useful for developing skills in problem solving. Being put in a novel situation and trying to understand the fundamental structure which unlocks the solution — as demonstrated at Finding Fifteen — is at the core of mathematical thinking. One particularly deft problem-solver is mathematician Tanya Khovanova (b. 1959), who received silver and gold medals at the International Mathematical Olympiads before earning her PhD in super-integrable systems from Moscow State University. She currently conducts research in recreational mathematics. Dr. Khovanova is now a Lecturer at the Massachusetts Institute of Technology who is active in helping high school and middle school students become world class math researchers, too.

Kathleen Mary Ollerenshaw was born in 1912 in the United Kingdom. She combined careers as a mathematician and politician despite being deaf from the age of eight. She published over 25 mathematical papers and wrote on magic squares with mathematician and cosmologist Hermann Bondi. In 1982, they published a paper about 4×4 normal magic squares in which they proved the conjecture of Frénicle de Bessy showing that there are 880 essentially different normal magic squares of order four.
Kathleen served in a variety of government posts and in 1970 was awarded the title of Dame of the British Empire by the Queen for her work in education.
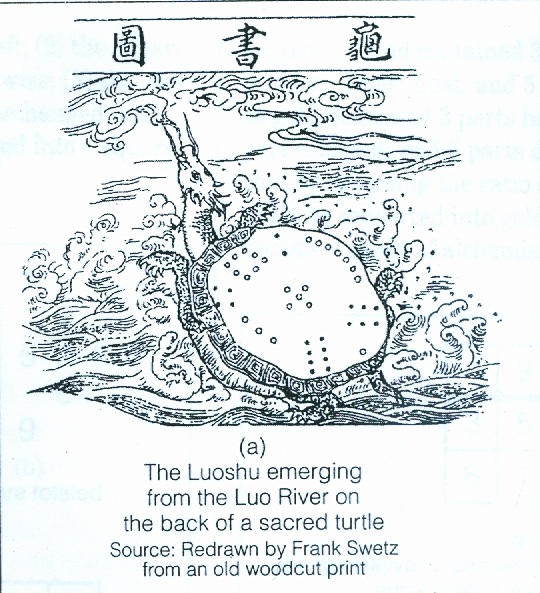
Legend has it that there was once a great flood in ancient China that destroyed many crops and much land. Every time the river Lo flooded, the people made sacrifices to calm the river. A tortoise would crawl out of the river and walk around the sacrifice. One day, a child noticed a pattern of dots on the tortoise’s back. The pattern was a magic square with magic constant 15! The people then knew that they must make sacrifices to the river for 15 days to calm the river.
This mysterious array, known as Luoshu, is considered a clue to early Chinese civilization. It is believed to have originated in Henan Province in Central China about 4000 years ago. The Luoshu (or Lo Shu) is a 3×3 magic square with numbers are represented by dots. Count the dots to find that the first row is 4, 9, 2; the second row is 3, 5, 7; and the third row is 8, 1, 6.