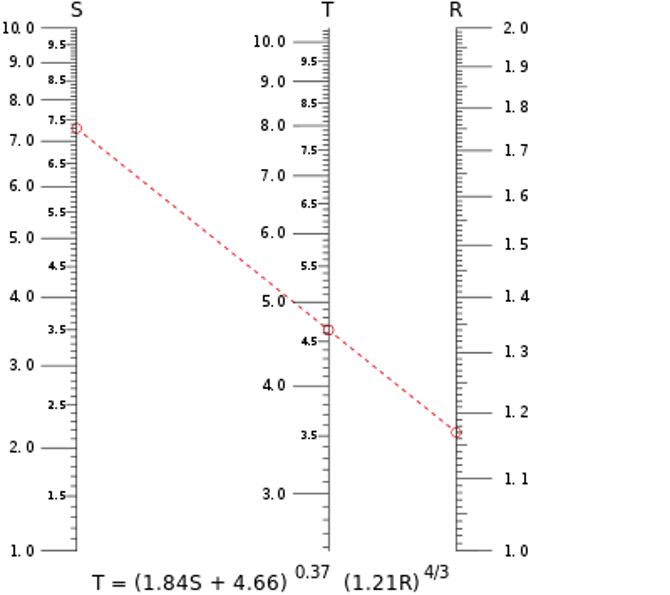
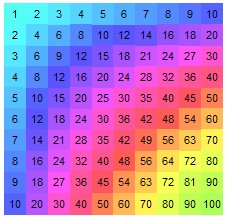
String Product only has buttons corresponding to whole numbers between 1 and 10 – meaning, there aren’t any fractions or decimals marked on String Product.
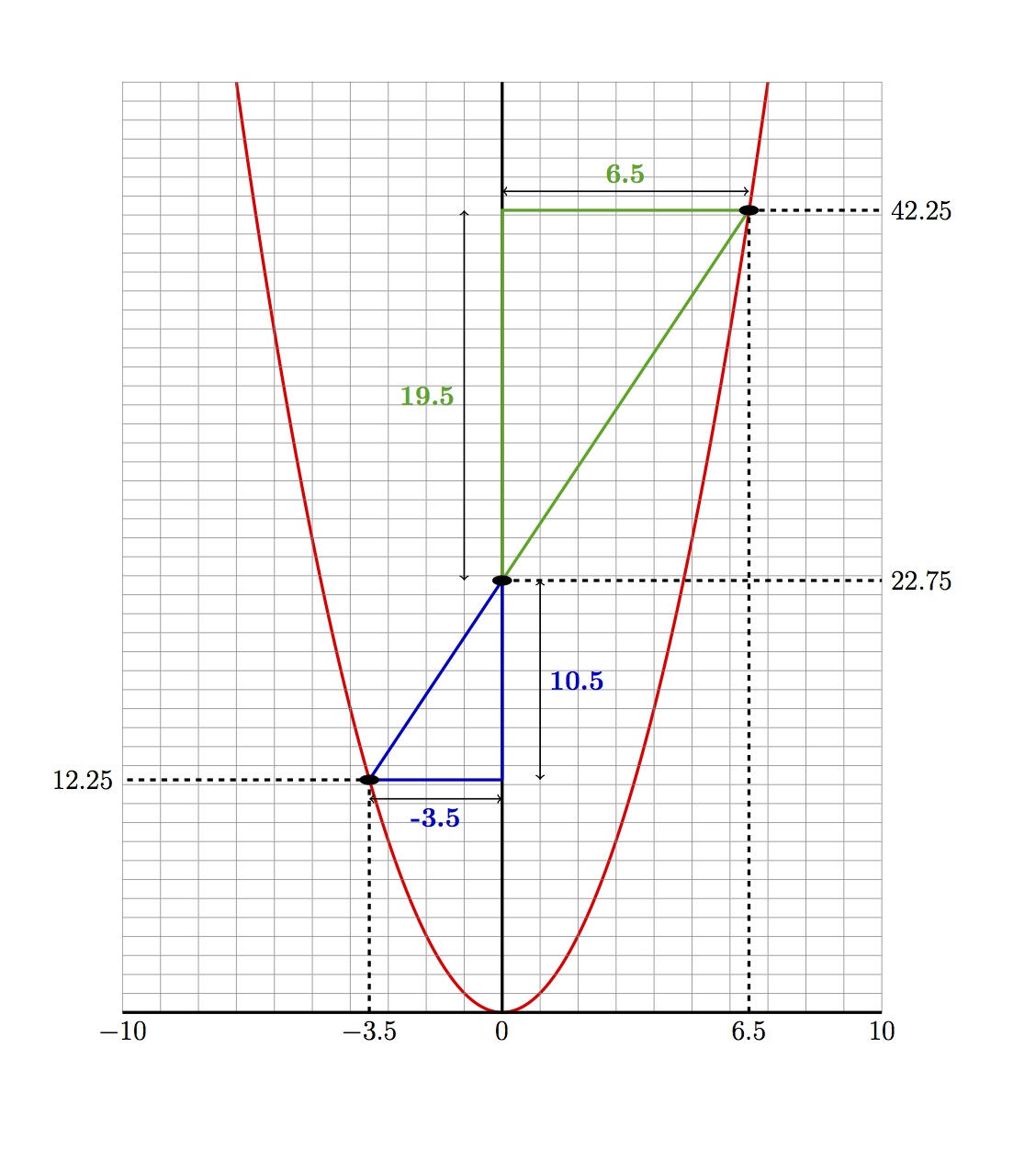
But just because the fractions aren’t marked doesn’t mean they aren’t there! Picture where the ring on String Product for 4 1/2 would be. Follow the imaginary line between 4 1/2 and 6.
How can String Product be used to approximate 6×4 1/2?
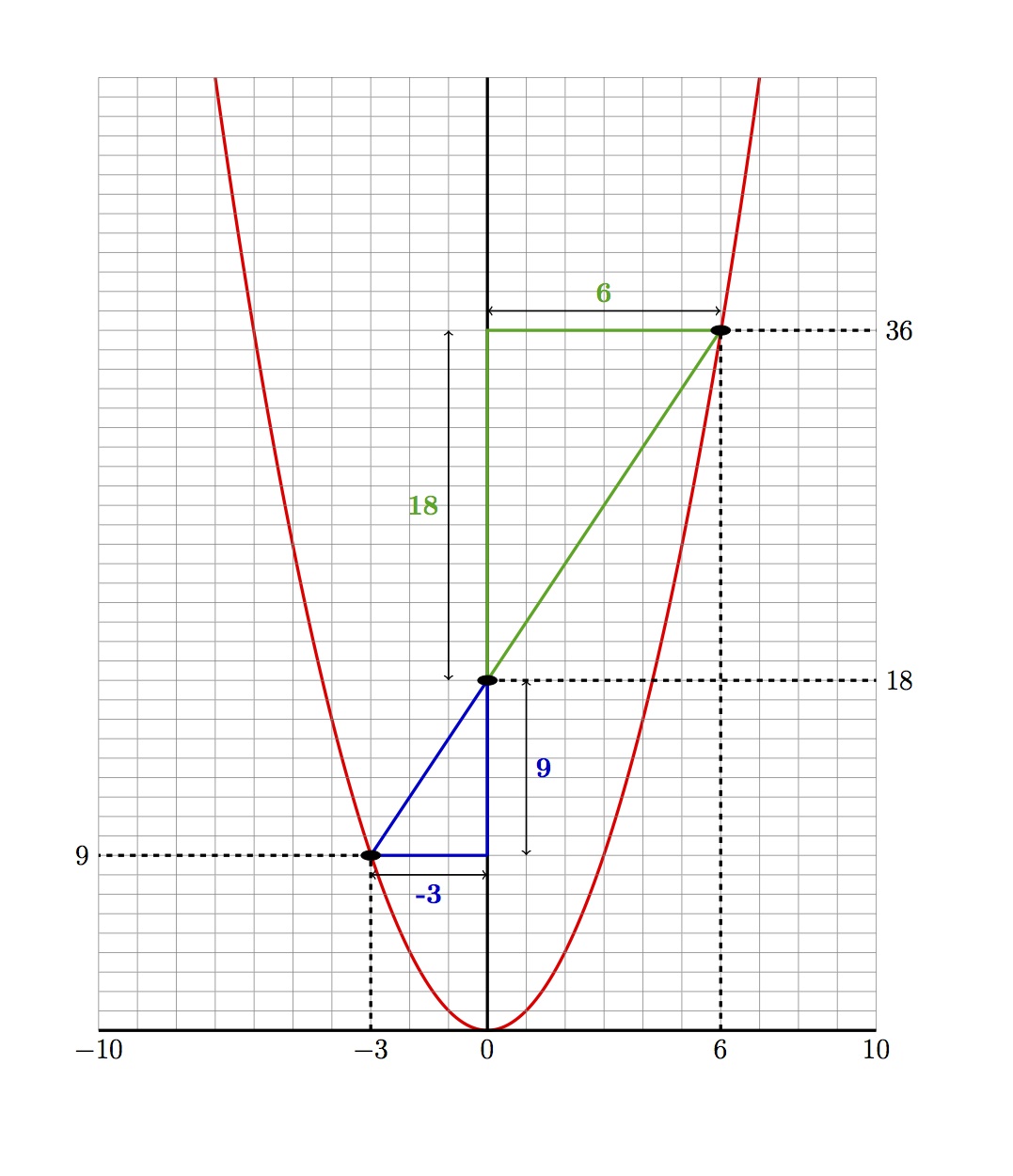
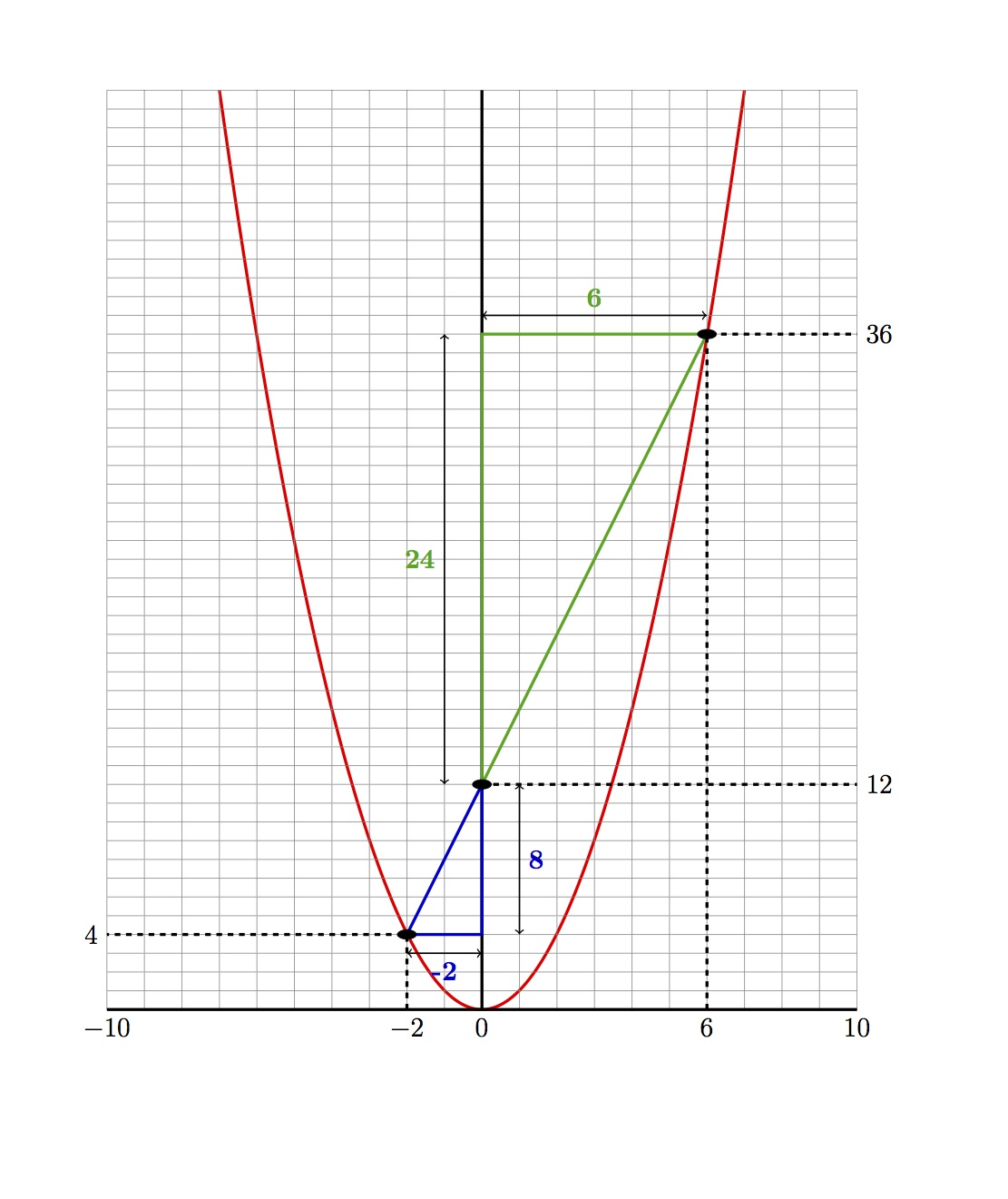
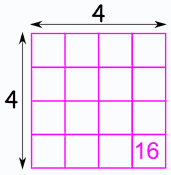
Find a colored wire that connects a numbered ring to itself. These wires cut right across the String Product, parallel to the floor. They represent two of the same number being multiplied together. The results are called perfect square numbers.
Think about finding the area of a square – the length of a square is the same as its width, so to find the area, two of the same number are multiplied together. That’s where the name “square number” comes from.
For example, look at the wire connecting 4 with itself across the circle. When that wire passes through the middle of String Product, it touches the number 16, which is 4 x 4. Use the String Product to find all of the perfect squares, starting with the smallest.
Wonder why String Product is shaped like a giant, skinny bowl, or like a revolving “U”? It has everything to do with those square numbers.

Romanian mathematician Alexandra Bellow (b. 1935) received her PhD from Yale under Kakutani and spent most of her career at Northwestern University, studying ergodic theory, probability, number theory, and analysis. Though she surely knew her times tables from a young age, she would enjoy letting a parabola do all the work!

Oppenheimer Funds provided support that made String Product possible.
The nomogram was invented by mathematician Maurice d’Ocagne in 1880. Nomograms were mostly used by engineers and other people who needed to do complicated calculations in their jobs. Nomograms often looked a lot like String Product. They were made of several number lines, with the numbers layed out on them according the the type of calculation that the nomogram would be used for. Like in String Product, or on a thermometer, the user would pick the two numbers being used in the calculation, on two of the three number lines, and draw a line through them. Where the line crossed the third number line was the solution to the calculation.
Each different calculation requires a different nomogram. (While thermometers are great for telling temperature, they won’t multiply like String Product does.) A nomogram also only gives approximate answers. The accuracy of the answer depends on how well the scales on the nomogram are made, and on how well the user can draw a straight line. And, depending on the calculation, they can get pretty complicated.