
Where else besides the Museum of Mathematics can you be surrounded by so much math? Everywhere! No matter where you go, there are patterns, systems, shapes, and phenomena that can all be described by math.
The images in Seeing Math are just the tip of the mathematical iceberg. Notice the tessellations that appear in works of art and as patterns on fish. See the geometric shapes in the red cage fungus and in the skyscrapers and bridges. What other mathematical concepts can you see in these pictures?
Where will you find math after you leave the Museum?

This fungus grows naturally into a shape that looks like a slightly deformed sphere or spheroid. This spheroid is made up of connecting tubes in the shape of polygons.
We see pentagons, hexagons, and heptagons in this fungus. These polygons tile the whole spheroid without leaving any gaps or overlapping at all. A tiling pattern with these properties is called a tessellation.

The shape of this sculpture looks like a minimal surface. A minimal surface is a surface that has the least possible surface area for a surface with the same boundary. One way to think of a minimal surface is as the shape of that a rubber sheet would stretch into when its edges were held in place.
The boundary of this surface is made up of the three openings in the sculpture.

This fish is covered in a geometric pattern that includes hexagons.
A polygon is regular if all of its sides are of equal length and all of its angles are of equal measure. The hexagons on this cowfish appear to be regular hexagons.

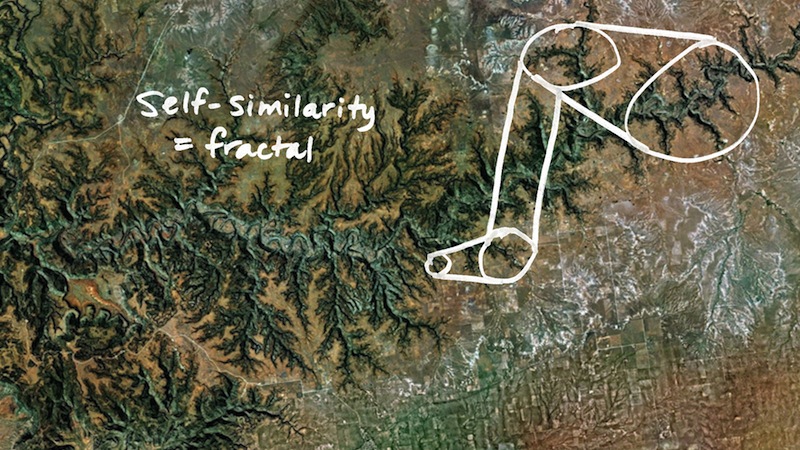
This satelite image of the earth shows the fractal nature of rivers. Fractals are shapes that contain smaller and smaller copies of themselves. Zooming in closer and closer on the river reveals shapes that look the same. This property is called self-similarity. Fractals are shapes that possess self-similiarity.
Parallel lines do not intersect, right? It’s not always so simple!
The edges of these New York City skyscraper are parallel, but they look like they will intersect if we continue drawing the lines into the sky past the buildings. In fact, all of the lines drawn on the picture look like they will intersect at the very same point!
Observations like this lead to the study of projective geometry, a branch of geometry where parallel lines do intersect!

The twisted shape of this bridge looks like it is tracing around a surface called a helicoid. A helicoid is a corkscrew-like surface that contains a helix through every point.
The equation written on this slide is for a helicoid surface.
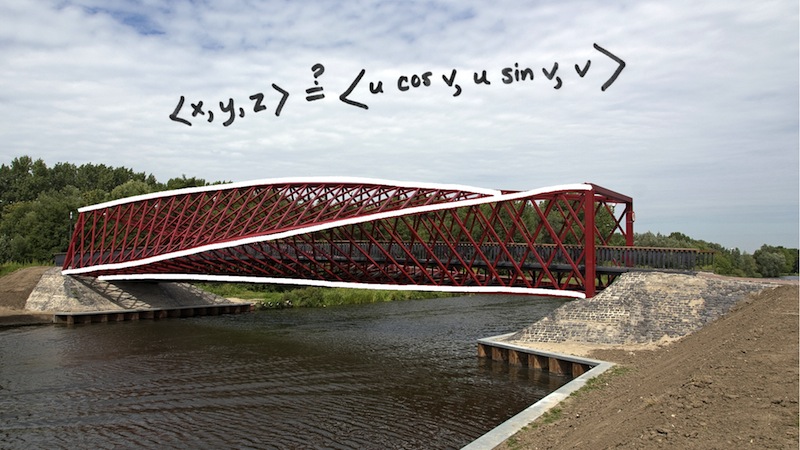
The notes on this photograph of a pyramid in Giza, Egypt highlight the geometric structure of the pyramid. Because this pyramid has a square base it is called a square pyramid. The apex, or top, of the pyramid is directly over the center of the square base, so we call this a right square pyramid.
The precision with which it was built makes it tempting to figure out the angle at the top of each side!



Red Cage Fungus (Ileodictyon Gracile) is a rare Australian stinkhorn.
Photographer: Carol Knudsen
Location: Australia

Green Void is a 20 meter high and 300 cubic meter topological sculpture created by the Labratory for Visionary Architecture (LAVA).
Photographer: LAVA
Location: Custom House Syndey (Sydney, Australia)

Honeycomb Cowfish (Acanthostracion Polygonia) has hexagonal patterned body.
Photographer: Wolfram Sander
Location: Havana, Cuba

Google Earth image by Paul Bourke.
Location: USA

Photograph of Midtown Manhattan skyscrapers.
Photographer: Cindy Lawrence
Location: New York, USA

Photograph of Double Helix Bridge.
Photographer: Pieter can Marion

Photograph of Great Pyramid at Giza.
Photographer: Cannergy
Location: Giza, Egypt

Sculpture: “Equinox” by Charles O. Perry
Photograph by Cindy Lawrence.

Melanie Matchett Wood (b. 1981) is a Professor of Mathematics at Harvard, after being Chancellor’s Professor of Mathematics at UC Berkeley and Vilas Distinguished Achievement Professor of Mathematics at the University of Wisconsin. Like this exhibit, her work shows the amazing ways deep mathematics arises where you might least expect it.



