
Pattern Pants is designed to work with the exhibit Polypaint next to it. With Polypaint you can design repeating patterns and then with Pattern Pants project them onto your clothing. But Pattern Pants also has some patterns built into it that work independently of Polypaint.
All of these patterns show symmetry, which means that they repeat in one or more ways. For example, some of the patterns are the same if you slide them right or left or up or down or sometimes along a slanted line. Others have parts that look like reflections in a mirror or are created by rotating one part around a point. Compare some of the patterns and try to see what kinds of symmetry each one has.
Many objects in nature (including ourselves) and in art have various sorts of symmetry. The picture shows some from ancient Egypt. See the More Math section here and for Polypaint for further explanation of how symmetry works.

Mathematicians have classified the various sorts of symmetry that a pattern can have.
There are four basic types illustrated in the diagram. A pattern has translational symmetry if sliding it in some direction the right distance leaves it looking the same. All of the patterns in Pattern Pants and Polypaint have translational symmetry in two directions.
A pattern or object has rotational symmetry if rotating it by or some other angle leaves it the same. An object has reflection symmetry if some parts of it look as they are reflections in a mirror of other parts. The fourth kind of symmetry is called glide reflection symmetry and is a combination of a reflection and a translation.
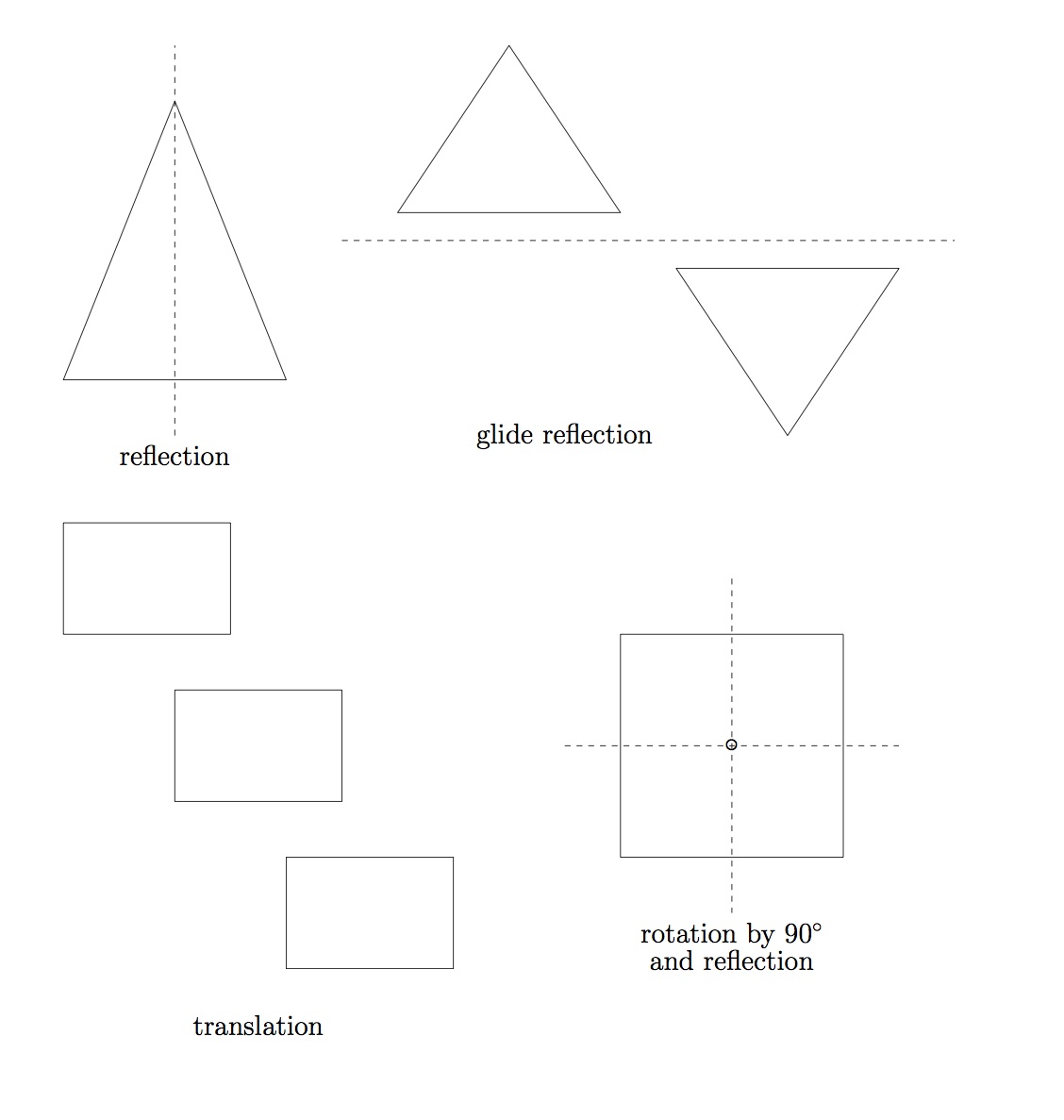
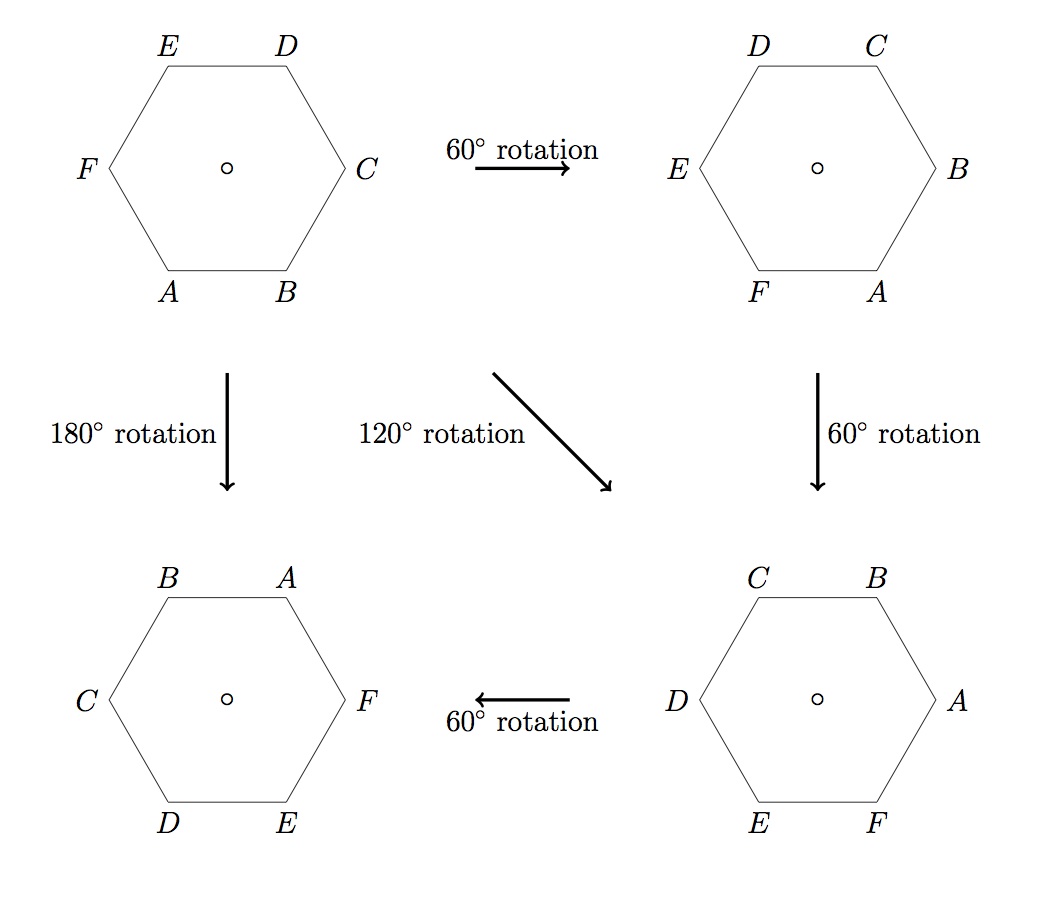
Every symmetry of a 2-dimensional figure is a combination of these four types. The action of performing two of the symmetry actions is again a symmetry as illustrated here by rotations of several angles.
One of the surprising facts uncovered by studying these patterns using tools of mathematics is that all of these possible combinations fall into one of just 17 types. Although artists have been using these patterns for thousands of years in societies from the most primitive to the most developed, it was only in 1891 that the Russian mathematician E. S. Federov proved that there are exactly 17 of these so-called symmetry groups.
The image here shows how a simple repeating wave figure generates 17 different patterns when these symmetry groups are applied. The first pattern has only translational symmetry, the second has rotational symmetry (how many degrees are the rotations and what points are they around?) and the third has only reflectional symmetry (what lines are the reflections in?). Look at the other patterns and try to see which of the symmetries each one has.
The 17 types of symmetry are also illustrated and described on the website
http://www.clarku.edu/~djoyce/wallpaper/index.html


This is one of the many types of patterns that we can make, taken from a wallpaper in the Alhambra palace in Spain. Notice how the heart-shaped logo zigs and zags between two different columns, giving lots and lots of symmetry.


Jhane Barnes is an award-winning successful textile designer and men’s clothing designer. She has a team of mathematicians who take her design ideas and use software programs that can repeat the designs using symmetry groups or other manipulations that can break some symmetry, modulate colors, and more. Software then translates the textile designs into Jacquard loom directions so that the patterns can be woven.

American mathematician Euphemia Haynes (1890 – 1980) received her PhD while studying certain symmetry correspondences, not unlike the patterns in this exhibit. She went on to be an active champion of school-age mathematics and training, and to establish the mathematics department at University of the District of Columbia.


