
Make your own version of the Museum’s logo! Pick a symbol from the slider at the top. Then use the knob and lever to change the size, shape, and position of your symbol. The computer makes copies of your symbol all around the circle.
The most beautiful logos that visitors make will be shown from time to time in the Museum. Enjoy!

Group theory is the branch of mathematics that studies symmetry and the relationships that govern different kinds of symmetry. For example, with the reflection and rotation symmetries in this exhibit, reflection in a line, followed by reflection in a perpendicular line, is equivalent to a half-turn rotation. Many other types of symmetry are possible, beyond the rotation and reflection symmetries used in this exhibit. Translational symmetry arises from moving an object through space, whether in one, two, or three dimensions. In three dimensions, rotation and reflection symmetry become much more complicated than in the two dimensions of this exhibit. Symmetry patterns described by group theory are extremely important in art, science, and technology.
A good book about where you can learn more about group theory is Visual Group Theory by Nathan Carter.

Logo Generator exploits the symmetry found in finite geometry, a focus of the research of Puerto Rican mathematician Minerva Cordero. Dr. Cordero is a Professor of Mathematics at the University of Texas at Arlington, where she is also the University’s Senior Associate Dean for the College of Science.

Stephen Wolfram is the founder and CEO of Wolfram Research, Inc., which produces Mathematica, the software package powering the MoMath Logo Generator.
Dr. Wolfram provided valuable assistance with the development of this exhibit, and is a founding Trustee of the National Museum of Mathematics.

Christopher Carlson of Wolfram Research created the concept and software behind the MoMath Logo Generator exhibit. Jeremy Davis, art director at Wolfram Research, and Anastasia Tumanova, graphic designer, created the logo design. Michael Sollami assisted with the exhibit software.
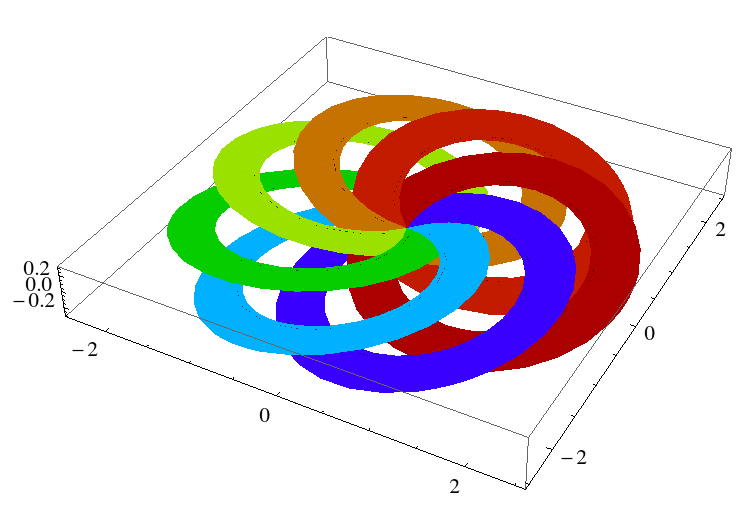
A Trustee of the National Museum of Mathematics and principal of Harbor Financial Management, Robert Frey is an accomplished applied mathematician and a member of the Stony Brook University faculty, directing the program on financial mathematics there. Dr. Frey suggested a key aspect of the operation of the Logo Generator, namely that in order to create this particular two-dimensional pattern, it is critical to think of the symbols as existing in three dimensions and choose a particular viewpoint to produce the logo. The image on this page shows seven circles handled according to this scheme, but from a different viewpoint.

Jade Vinson provided useful ideas and conversations for the design of the MoMath Logo Generator. Dr. Vinson was the recipient of the 1998 Morgan Prize from the American Mathematical Society, the first to solve the “holyhedron” problem, and as of 2013 became a Trustee of the National Museum of Mathematics.

Snowflakes are one of the most striking examples of physical symmetry. Because of the physical properties of ice, they have six-fold rotational symmetry, different from the eight-fold rotational symmetry of the logos in this exhibit. Because of the way that they grow in cold humid clouds, this symmetry is maintained as they grow; in addition, they generally have reflection symmetry about three different lines. (An area of mathematics called group theory tells us that if they have rotation symmetry, and at least one reflection symmetry, then they must necessarily have the other two reflection symmetries as well.)

The possible moves on a Rubik’s Cube form a mathematical structure called a group, and the study of groups, known as group theory, is essential to solving the cube. Each rotation of a face is one element of the group, and these rotations combine in various ways. For example, it is possible to calculate that the number of possible configurations is roughly 43 quintillion (43 x 1018); and yet, mathematicians have now figured out that it is always possible to solve any configuration, no matter how scrambled, in at most 20 moves.



