
Motionscape is a game that you control by changing your position and velocity on the track.
Adjusting your position is as easy as moving back and forth. The starting spot is considered position 0. Moving forward toward the front screen on the track increases your position and moving backward decreases your position. So a position of -2 just means two meters behind the starting position.
Velocity is the speed in which you are moving together with the direction in which you are moving. Positive velocities mean movement forward and negative velocities indicate moving backward away from the screen. Try moving backward and forward on the track at different speeds to guide your position and velocity graphs through the gates!
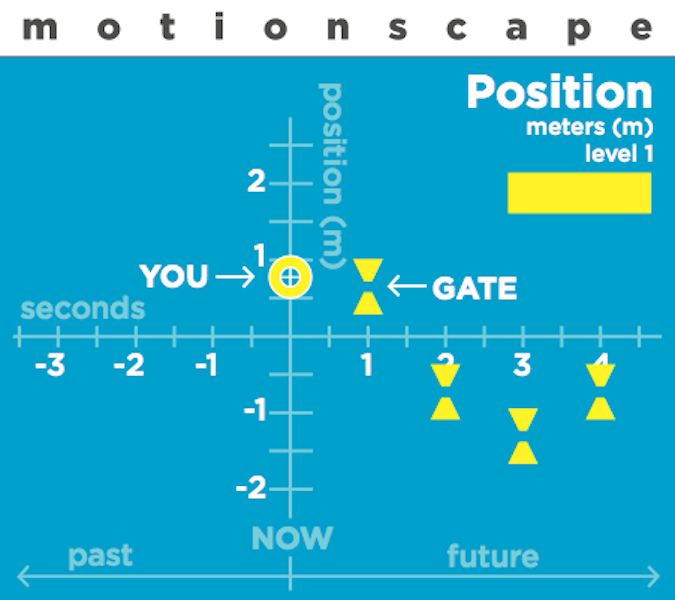
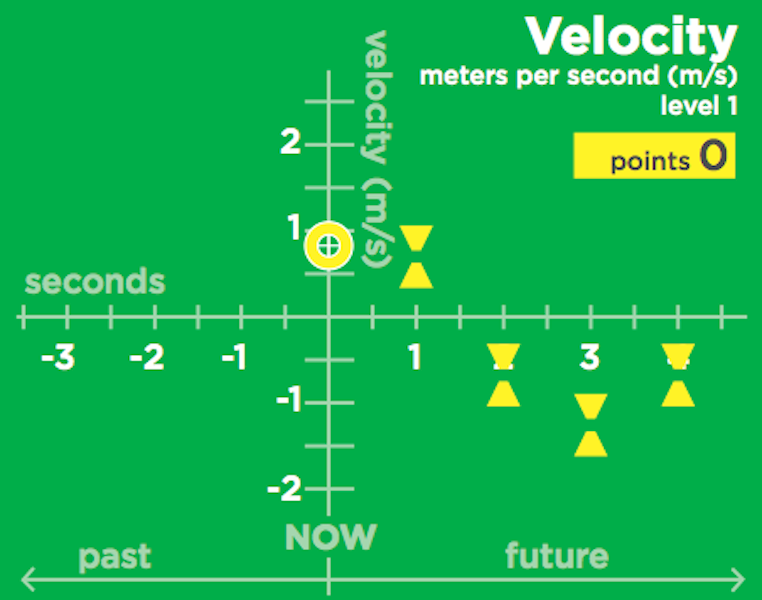
The three graphs in Motionscape show how three different quantities change in time.
The numbers like -3 and -2 with a “-” in front of them are called negative numbers. Numbers without this symbol (or with a “+”) are called positive numbers. The numbers you first learn in school are positive.
The first graph shows how your position changes in time. This shows where you were standing at different points of time. Positive positions are forward of the starting point on the track and negative positions are behind this point. The second graph shows your velocity. This is how your position was changing at each point in time. Velocity is a measure of your speed and the direction you were moving at that time (positive velocity means forward motion and negative velocity means backward motion). The third graph shows your acceleration through time. Acceleration is how your velocity is changing. Positive acceleration means that your velocity is increasing and negative acceleration means that your velocity is decreasing. Since velocity measures direction as well as speed your speed can increase even as your velocity decreases!

In order to launch anything into space, scientists use calculus to understand how objects behave when forces act upon them to make them move.

The mathematics that relates position to velocity and acceleration can be used to study geometric properties as well.

Biological systems involving predators and prey can be explained using calculus.

Rollercoaster designers use calculus to ensure that rollercoasters give a thrilling, but safe ride.

Motionscape was made possible thanks to the generosity of the attendees of MoMath’s Opening Ceremeny held on December 12, 2012, including David K.A. Mordecai & Samantha Kappagoda, Brittany L. Dwyer, Anoop Prasad, and Mr. Stephen Modzelewski & Mrs. Deborah Y. Sze.

One of the earliest popular textbooks in calculus — the topic of this exhibit — is due to Italian mathematician Maria Agnesi (1718 – 1799). Along with an asteroid and crater on Venus named after her, is also a particularly devilish curve, first described by Fermat, which now commonly goes by the name “Witch of Agnesi.”
Velocity measures how position changes as time goes by, and acceleration measures how much that velocity changes. The math used to relate position, velocity and acceleration is called calculus. Change happens in practically every real world situation, so calculus, the math of change, can describe rates of change in chemical reactions, population growth and prices of goods. These are just a few examples of how calculus is used to model and make predictions in science, business and engineering.

The distance from Earth to Mars is, on average, 225 million km (140 million miles). Mars is orbiting the sun at an average speed of 24 km per second (approximately 53,700 miles per hour) while Earth is moving along its orbit at about 30 km/s (approximately 66,600 miles per hour). That’s fast! And it’s not to mention the rotation of Mars and Earth on their axes.
In order to land the Curiosity rover on the surface of Mars, scientists needed to understand these movements very well. The relationships among position, velocity, and acceleration that you need to understand to beat the challenges at Motionscape were carefully studied by the scientists at NASA who launched this space craft from Earth and landed it on Mars where it took the self-picture displayed here.

Rate of change is one of the most important concepts in mathematics.
The rate of change of a quantity is called the derivative. Velocity is the derivative of position and acceleration is the derivative of velocity. Sir Isaac Newton (pictured top right) and Gottfried Wilhelm von Leibniz (bottom right) are credited with formalizing these ideas into what we now recognize as modern calculus in the late seventeenth and early eighteenth centuries, although many of the core ideas date back thousands of years.
As you walk, your position changes with respect to time. The rate at which your position changes is called velocity. As you speed up, slow down, or change direction your velocity changes. The rate at which velocity changes is called acceleration — a rate of change of a rate of change! We could even keep going (the rate of change of acceleration is called jerk.) These concepts are essential for describing physical motion.


Gottfried Wilhelm Leibniz was a German mathematician who lived from 1646 until 1716. His work has been highly influential in mathematics, philosophy, computer science, and many other fields of science for hundreds of years.
One of Leibniz’s biggest discoveries was how to find the area of shapes whose outlines are described by mathematical equations. He knew that the area of a rectangular region is the length times the width of the rectangle, but wanted to be able to find areas for many different shapes.
The method developed by Leibniz uses rectangles to approximate the area inside of an irregular shape.
The tools he developed to solve this problem are called calculus, and Leibniz was among the first people to develop them.
The symbols that Leibniz invented for his methods are still used today in calculus and algebra.

The mathematics relating position to velocity and acceleration is called calculus. This is a set of tools that allow mathematicians to relate a quantity to how fast that quantity is changing.
In the late 1600s and early 1700s, Sir Isaac Newton was one of the first people to develop the tools of calculus. Newton was a mathematician and physicist whose work became the basis for classical mechanics, which is the study how things move. He discovered how to use math to model how objects behave when they fall or roll or fly or move in any way. He formulated laws that govern how objects move that are called Newton’s Three Laws of motion and was among the first scientists to understand gravity.
Newton’s work in physics and the tools of calculus continue to be fundamental to how we understand the world today.


Here you is a link to a collection of Isaac Newton’s papers and publications. You can see some of his handwritten notes and calculations.
http://cudl.lib.cam.ac.uk/collections/newton
Note that Newton sometimes wrote in Latin, which was the norm for academic writing from that period of history. Please see the next entry in this section for an English translation of Newton’s Principles of Natural Philosophy.

At the following location you can read through an English translation of Isaac Newton’s Mathematical Principles of Natural Philosophy, also called The Principia, in which he develops fundamental laws of the physics of motion, including explaining his theory of gravity.
http://books.google.com/books?id=Tm0FAAAAQAAJ&pg=PA79#v=onepage&q&f=false


