
Sit in the chair at Hyper Hyperboloid and look around you. What do you see? What shape do the cords around you make?
Now spin your chair. As you spin more and more, what happens to the cords around you? Do they change shape? Is the shape that the cords make together changing?
The curved surface that is formed when the chair is twisted is a single-sheeted hyperboloid. It is a special surface because it can be made out of straight lines. In fact, this surface can be made out of straight lines in two different ways, one represented by the red cords and one by the yellow cords. It is one of only three surfaces that have this very special property!
Once you spin the chair, the shape made by the cords is no longer a cylinder. The shape you see is called a hyperboloid. When the chair is spun all the way around, the shape made by the cords is a cone. Hyperbolids and cones are both examples of special kinds of shapes called quadric surfaces.
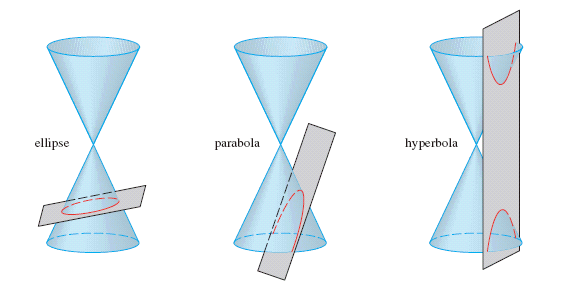
Before talking about quadric surfaces, let’s imagine their simpler cousins, conic sections. Conic sections are curves that we can find by looking at the shapes we see when we slice a cone with a plane. (See the diagram.) Some conic sections are very familiar shapes, like circles and ellipses. Others are more exotic, like parabolas and hyperbolas.
How would you slice a cone to get a circle? How would you slice it to get an ellipse?
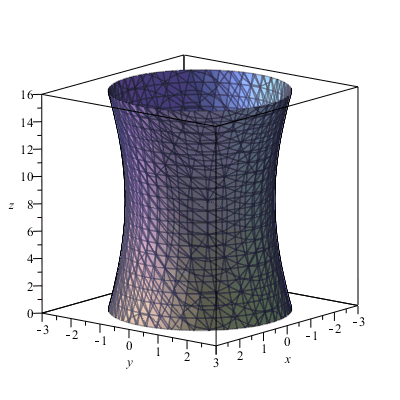
Here is an example of a hyperboloid. If the cords at Hyper Hyperboloid make a cylinder when you sit down, you can form this hyperboloid by rotating slightly in the chair.
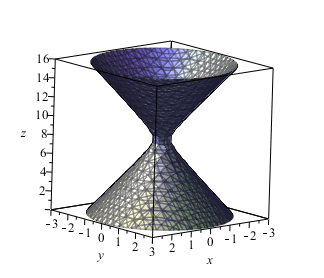
As you continue swiveling, the concentric cylinders continue to narrow in the middle. After spinning a half turn in the chair, the cords around you make a hyperboloid like the one you see in this picture. Does this hyperboloid look more like a cylinder or a cone?

Here is a picture of the Didcot power station (UK). The power station has hyperboidal cooling towers.

This hyperboloid of one sheet formed out of skewers was created during a math enrichment class run by George Hart. In fact, this construction activity appeared in the Math Monday column on the Make Magazine blog from the Museum of Mathematics!

This is the Canton Tower in China.

Creating a curved surface using only straight lines would be right up the alley of American mathematician Mina Rees (1902 – 1997), who served as Head of Mathematics at the Office of Naval Research. While there, Rees oversaw a variety of research programs, including studying hydrofoils, logistics, computers, and numerical development for applications such as rocketry and defense against submarines. Her distinguished career as researcher, administrator, and leader saw her receiving a whopping 18 honorary degrees, and serving as president of the American Association for the Advancement of Science, and as founding president of the Graduate School and University Center at City University in New York.
Quadric surfaces – like the cylinders, hyperboloids, and cones at Hyper Hyperboloid – which are graphed in three dimensions are analogous to conic sections which are graphed in two dimensions.
Conic sections were studied extensively by Apollonius of Perga in ancient Greece, and they played a major role in the development of scientific theories through the ages. For example, Apollonius’ ellipses were studied extensively by Kepler in the late sixteenth and early seventeenth centuries. The ellipses played an important role in Kepler’s laws of planetary motion.



