FORMULA MORPH
You’ve probably heard of a formula before. There are formulas to make and find all kinds of things. Did you know that there are formulas that turn numbers into twisty, curvy shapes?
Choose a shape and formula by rolling the silver wheel. Each formula will have different numbers that you can change. Turn the lighted knobs to adjust the numbers in the formula and watch happens to the shape on the screen!
Can you find a knob that makes the shape taller? That makes the shape fatter? That adds bumps and waves, or takes them away? What happens when you turn more than one knob?
The shapes on the right and left sides of the screen are created by museum visitors. Those two shapes combine to make the shape in the middle. Move the lever in the center of the console from the left to the right to watch the shape morph!
How does a formula describe a surface? First, a surface is made up of points; the formula will tell us which points are on the surface.
A point in space can be described by three numbers that measure how far the point is in each direction from a point in the center called the origin. You might think of these numbers as measuring distance in the directions East-West, North-South and Up-Down.
In the diagram, the point (3,4,5) is 3 units East from the origin, 4 units South and 5 units Up. Below it is the point (3,4,0) with the same distances on the ground but no height. Of course, it takes a bit of imagination to think of this flat picture as representing three-dimensional space!
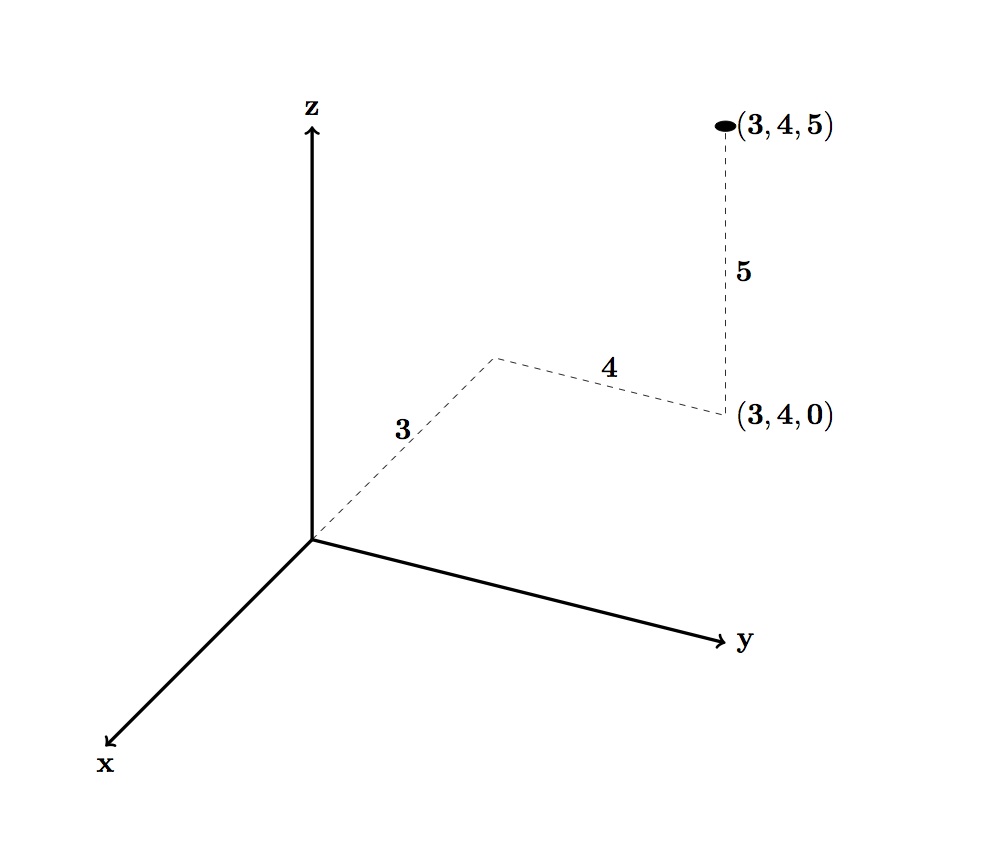
Notice that all of the formulas in addition to numbers have three letters, called variables, x, y and z — for example 2×2 + 6y – z. Now given a point, such as (3, 4, 5), we can put the three numbers into the formula in place of the variables — 2 x 32 + 6 x 4 – 5 (in the formula we don’t have to write the multiplication sign, but with numbers we do) — and then do the arithmetic: 2 x 9 + 6 x 4 – 5 = 18 + 24 – 5 = 37. Since the result is not 0, we conclude that the point is not on the surface described by the formula. Can you find a number w such that the point (3, 4, w) is on the surface?
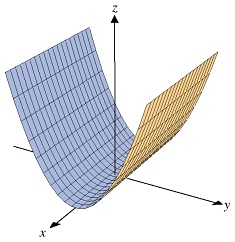
Now consider the formula y2 – z = 0 (there’s no x but it’s the same as having a term 0x). An equivalent way to write this is y2 = z. A point is on the surface described by this formula if it’s height (in the direction of the arrow labeled z) is the square of its distance in the direction of the arrow labeled y (remember y2 means y times y and is called y-squared). For example, the point (3,4,16) is on the surface because 16 is 4-squared. Can you find some other points on this surface?
If you have looked at the exhibit String Product you may notice that this is a similar shape; although it’s a bit different, the cross-section is the same shape called a parabola.
Here’s another simple example; this one is described by the formula x2 + y2 – z2 = 0. If a point is u units in the x-direction and v units in the y-direction, then its direct distance from the center is w such that w2 = u2 + v2. This is just the Pythagorean Theorem which you may have seen in an exhibit on the lower level. So to be on this surface a point is just as far up (or down, since negative numbers have the same squares as their positive counterparts) in the z-direction as it is away from the center. The z-distance is constant along circles since those consist of points all the same distance from the center.
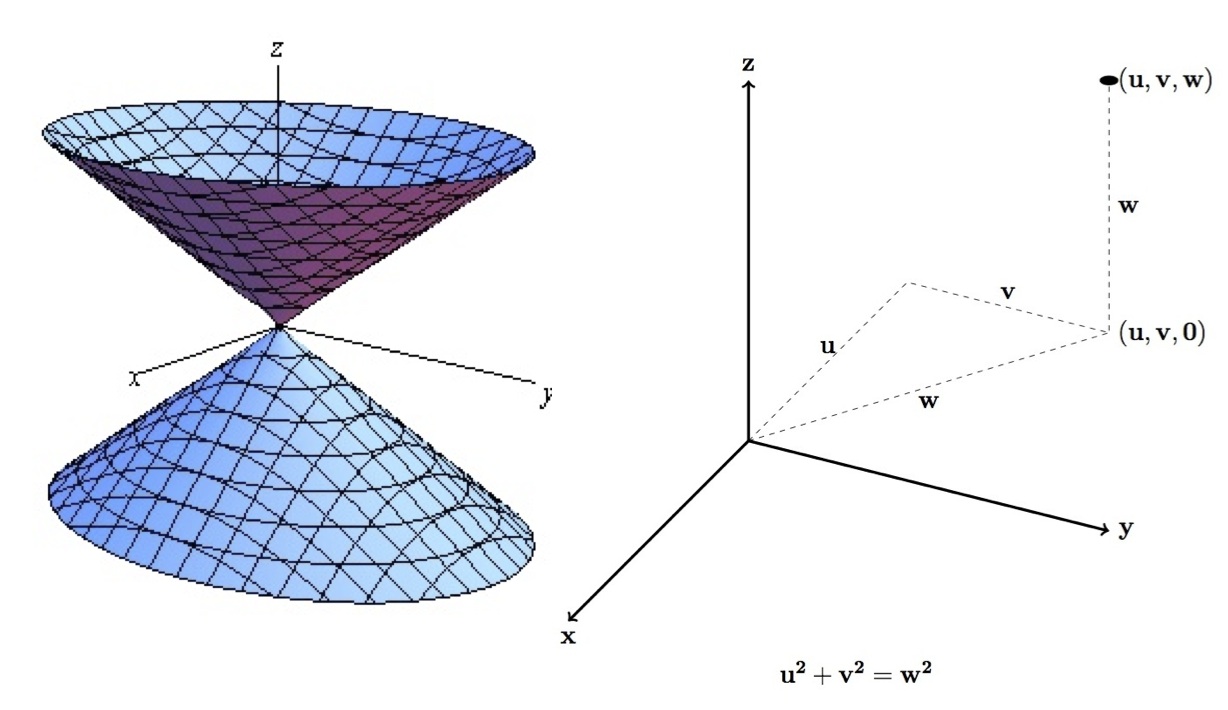
Now, if this surface were on the machine we would be able to move the dials to change the surface to be the one with formula ax2 + by2 – cz2 = 0 for different values of a, b and c. For example, points on the surface with formula 3×2 + 3y2 – z2 = 0 would be 3 times as far in the z direction as they are out from the center so the cone would be narrower and thinner. The diagram shows these two surfaces. What would happen if we make c bigger? Think about other variations.


The Mathematisches Forschungsinstitut Oberwolfach
The Mathematisches Forschungsinstitut Oberwolfach is located in the German Black Forest. It was founded in 1944 and has developed over the years into an internationally renowned research institute. In mathematical research, interchange of ideas plays a central role. The high degree of abstraction of mathematics and the compact way it is presented necessitate direct personal communication. Although most new results are nowadays quickly made available to the mathematical community via electronic media, this cannot replace personal contact among scientists. The importance of personal contact can only increase with the constant increase of specialization. Therefore, the Institute concentrates on cooperative research activities of larger groups (workshop programs) or smaller groups (mini-workshop programs and Research in Pairs). In all activities, participation of promising young scientists plays an important role. Every year the institute hosts about 2,500 mathematicians.

Julia Robinson1919 – 1985
David Hilbert famously asked whether a “formula,” or rather, a system of algebraic equations, as in this exhibit, has solutions with all unknown variables being integers. American mathematician Julia Robinson (1919 – 1985) and her collaborators decisively answered Hilbert’s question in a most profound way: it is impossible, in general, to tell! For this work and much else, she received the MacArthur “Genius” Award along with many other accolades.

The Klaus Tschira Foundation
The Klaus Tschira Foundation supported the SURFER team in their efforts to bring Formula Morph to fruition.
The Klaus Tschira Foundation was established by the physicist Klaus Tschira in 1995 as a non-profit organization. Its primary objective is to support projects in natural and computer sciences as well as mathematics. The Klaus Tschira Foundation places strong emphasis on the public understanding in these fields.

SURFER Team
Formula Morph is part of IMAGINARY, an open source platform for interactive mathematics by the Mathematisches Forschungsinstitut Oberwolfach. It is based on the program SURFER, a raytracer for algebraic surfaces in real time. The SURFER software package, developed at Mathematisches Forschungsinstitut Oberwolfach, is used to plot the surfaces you see in Formula Morph.
The SURFER team responsible for this package was: Gert-Martin Greuel, direction; Christian Stussak, programming; Andreas Daniel Matt, coordination and content; with thanks to Valentina Galata, Herwig Hauser, Stephan Klaus, Oliver Labs, and JLaTeXMath.
SURFER can be downloaded for free at the IMAGINARY platform: http://www.imaginary.org

