
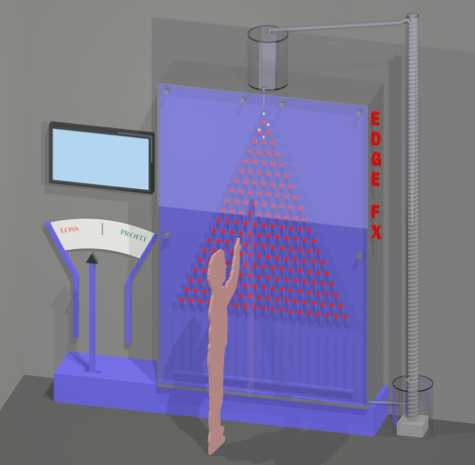
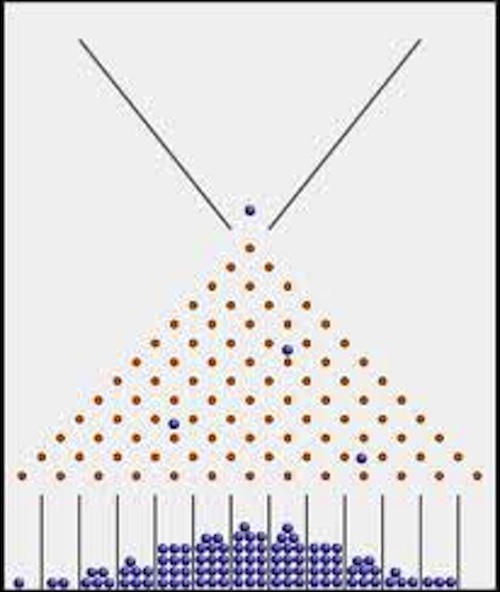
Set the lever in Edge FX to the center and push the button to unleash a cascade of balls. Each time a ball hits a peg, it has an equal chance of falling either to the right or to the left.
Pushing the lever to one side moves the peg blockers, making it more likely for a ball to fall to one side than the other. How does a change in the lever’s position affect the stacks of balls at the bottom of Edge FX?
Explore Edge FX and learn just how predictable a series of unpredictable events can be!
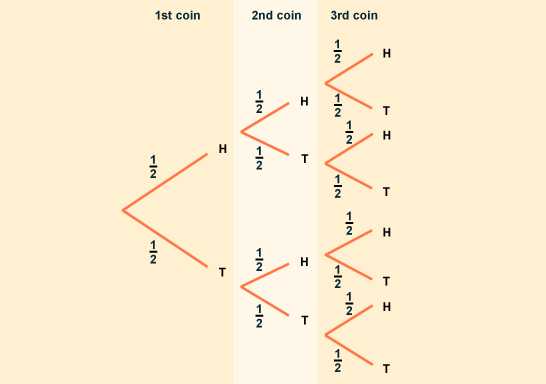
Suppose you tossed a coin two times in a row and it came up heads each time. What are the chances it will come up heads on the next toss? What if we changed the question and asked what are the chances of tossing a fair coin three times and getting heads each time? The answers are quite different!
In the first case, the answer is 50%. The coin doesn’t know it has landed heads the previous two times; each time it is tossed there is an equal chance of it coming up heads or tails. But when we consider the likelihood of a succession of events, like three heads in a row, we have a different calculation to make.

For the first toss, there is a 50% chance of heads. But if we consider two tosses in a row, four things could happen: HH, HT, TH, or TT. Here “HT” means heads on the first toss, tails on the second. Four things could have happened, and we are interested in only one of them (HH). The chances of this occurrence are one out of four, or 25%. Each time we throw the coin again, we double the total number of possibilities from the last toss. For example, with three tosses, here are the possible outcomes: HHH; HHT; HTH; HTT; THH; THT; TTH; TTT. The probability of all heads is one out of eight, or 12.5%
What do you think the chances are of tossing a fair coin four times in a row and getting heads each time?

The Moody’s Foundation provided support that helped make Edge FX possible.

David Donoho is a professor in the Department of Statistics at Stanford University.
Dr. Donoho made useful contributions to conversations regarding concepts in probability related to Edge FX.

Following the trajectories of these bouncing balls would be a piece of cake for American mathematician Katherine Johnson (1918 – 2020), who worked at NASA calculating, among many other things, the orbital trajectories and launch windows for the Mercury, Apollo, and Space Shuttle missions.

James Propp is a professor in the Department of Mathematical Sciences at the University of Massachusetts Lowell.
Dr. Propp made useful contributions to conversations regarding concepts in probability related to Edge FX.


