POLYPAINT
Many decorative patterns consist of one or more smaller patterns modified in various ways and repeated across the area to be decorated; uses include floor coverings, wallpapers, pottery and other commonly decorated surfaces. Polypaint gives you the tools to design such patterns and to understand how they are constructed.
The right part of the display is a screen on which you can “paint” in several colors with an electronic brush. The left side has a number of patterns that determine how what you paint will be repeated. Try out the simplest patterns and a single stroke of the brush, then try to predict how other strokes will be repeated. Try different patterns with the same set of painted strokes. Notice that sometimes your painting is shifted or rotated or reflected as if in an invisible mirror.
Try to make a pretty design. When you have one you like, move over to Pattern Pants and see what it looks like projected on your clothing.

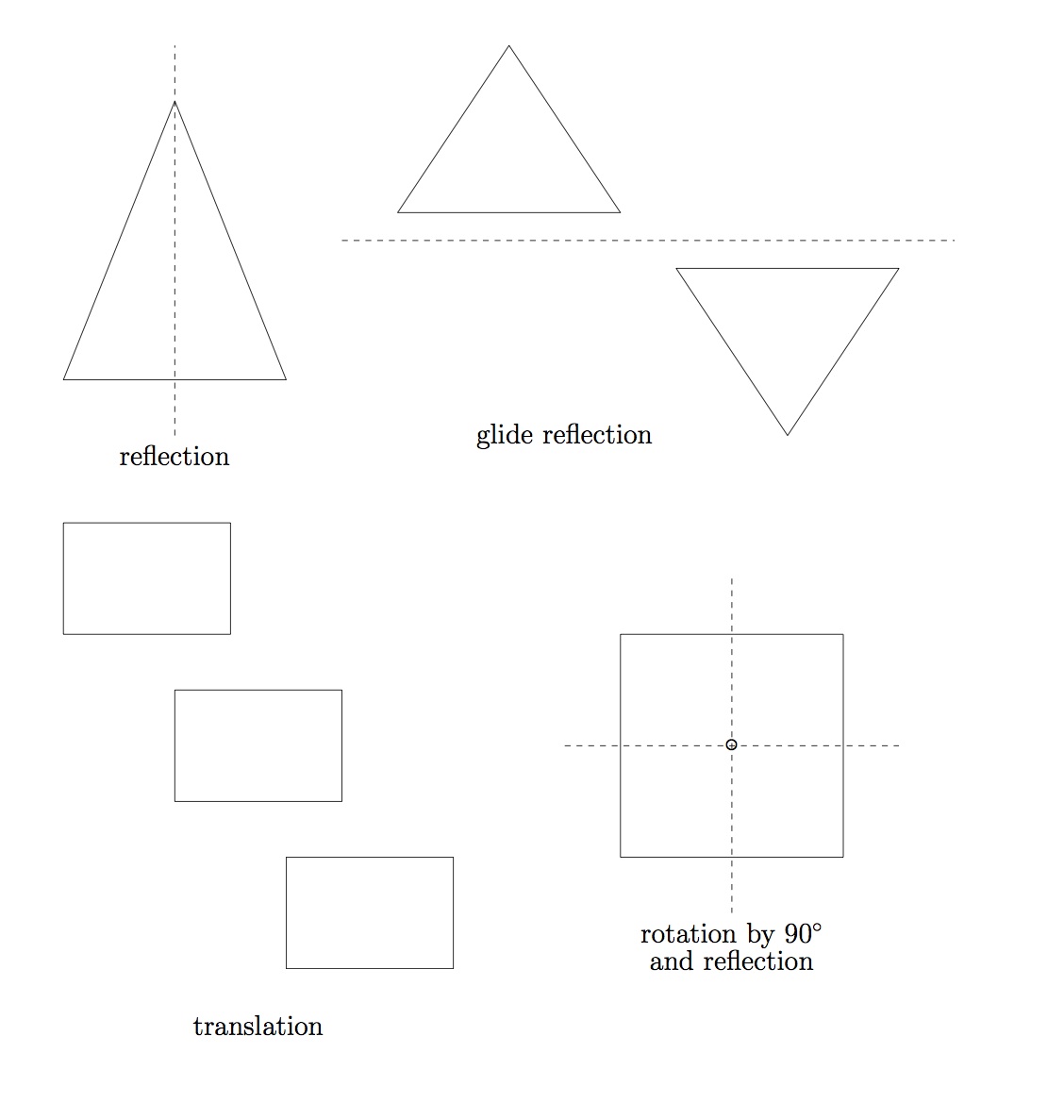
The mathematics behind Polypaint is the notion of symmetry. Patterns and objects are symmetric if moving them in various ways leaves them looking the same. Most animals, including humans, are (approximately) symmetric around a line down their middle; this is called reflectional symmetry since each side is like the other reflected in a mirror. Try some of the Polypaint patterns to find those with this kind of symmetry.
All of the Polypaint designs have translational symmetry — there are at least two directions in which you can slide (or translate) the design without changing it. Some of them are also symmetric with respect to rotations by 90 degrees or some other angle (rotational symmetry). The fourth kind of symmetry is called glide reflection symmetry and is a combination of a reflection and a translation.
Every symmetry of a 2-dimensional figure is a combination of these four types. Your choice on the right side determines which ones are built into the design that appears on the screen. Try several different ones and try to figure out which of these symmetries your design has.
Even though you can start with any strokes you like, it turns out that there is a limited number of different combinations of symmetries that the final design can have. The Russian mathematician E. S. Federov proved in 1891 that there are exactly 17 possible different combinations of symmetries, called symmetry groups.
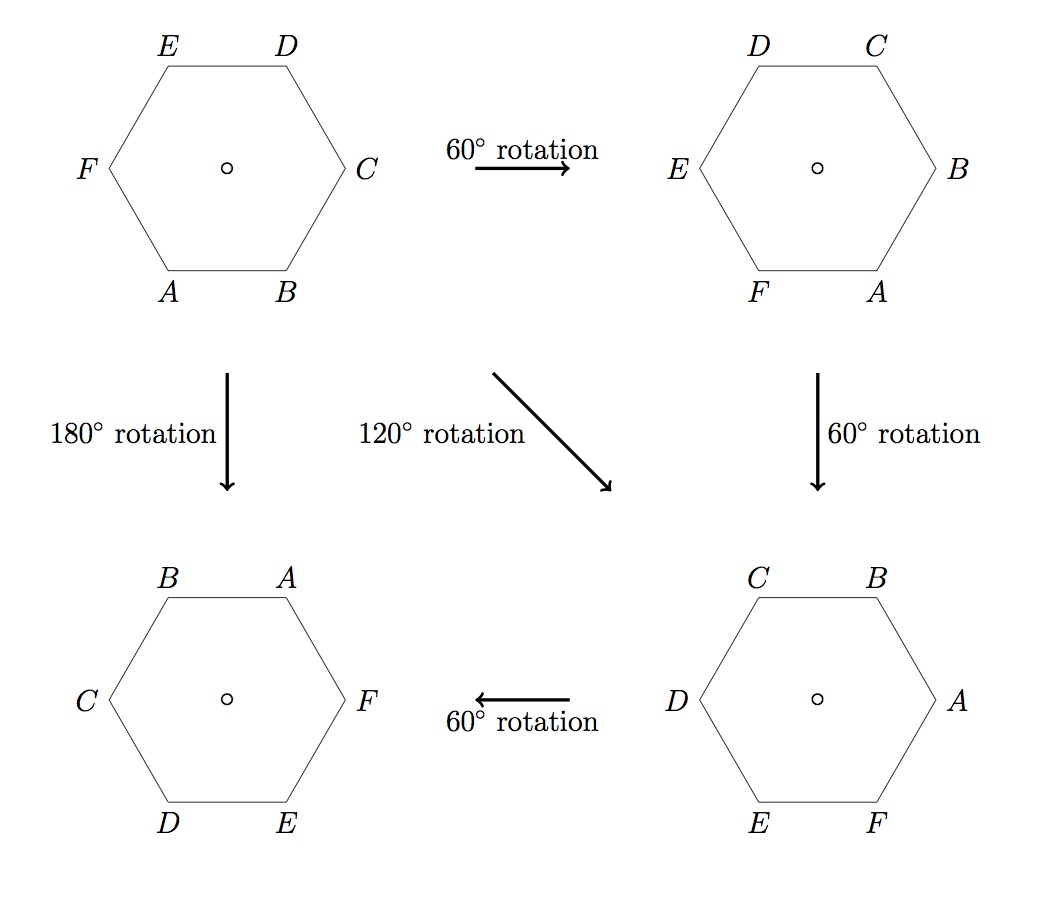
One of the surprising limitations is that rotational symmetry can only occur for a small number of angles: 60, 90, 120 or 180 degrees
Artists have been using these patterns for thousands of years in societies from the most primitive to the most developed. One of the most famous users is the Dutch artist M. C. Escher (1898 – 1972) who created amazingly inventive patterns. Very similar ideas are also used by scientists to classify natural rocks knows as crystals according to how the atoms are arranged.
The image here shows how a simple repeating wave figure generates 17 different patterns when these symmetry groups are applied. The first pattern has only translational symmetry, the second has rotational symmetry (how many degrees are the rotations and what points are they around?) and the third has only reflectional symmetry (what lines are the reflections in?). Look at the other patterns and try to see which of the symmetries each one has.


Notice the 4-fold rotational symmetry of this embroidery.


Fan Chungb. 1949Mathematics
The colorful patterns emerging from this digital canvas evoke the combinatorial and network structures studied by Taiwanese-born American mathematician Fan Chung (b. 1949), who worked at Bell Laboratories and the University of Pennsylvania before moving to the University of California, San Diego as the Paul Erdős Professor in Combinatorics.
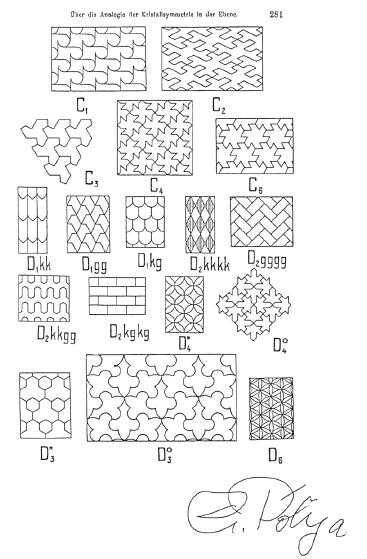
George Pólya1897-1985Mathematics
Although not the first to prove that there are exactly 17 plane symmetry groups, George Pólya was the first to illustrate these with representative tilings. It was this chart in Pólya’s 1924 article “Über die Analogie der Kristallsymmetrie in der Ebene.” in Zeitschrift für Kristallographie that M.C. Escher studied in 1937, spurring his investigations into how to create tessellations. Pólya’s notation for the symmetry groups is no longer used.
Evgraf Stepanovich Fedorov, a Russian crystallographer and mathematician, was the first to prove (in 1891) that there are exactly 17 plane symmetry groups. This was done, surprisingly, after he investigated the much more complicated problem of finding all three-dimensional crystallographic (or periodic) groups. In 1885, he proved there were 230 of these. Later other mathematicians and crystallographers, unaware of his work (publshed in Russian), proved there were 17 plane symmetry groups.


Kaleidopaint and iOrnamentAs soon as computers had drawing capability, there were programs to draw wallpaper patterns, driven by the action of symmetry groups. Many of these programs were exercises in computer science courses, others were published, and many went out of print as operating systems changed. Two excellent, current, and free apps for the iPad where you can make wallpaper patterns by drawing with your fingers are iOrnament, by Jürgen Richter-Gebert, and KaleidoPaint, by Jeffrey Weeks. iOrnament has a tutorial on the theory underlying the patterns and a display of historical patterns to explore. KaleidoPaint can display both the crystallographic notation or orbifold notation for the groups, show the underlying grid, and also color by symmetry.

Symmetries of CultureSymmetries of Culture, by Dorothy Washburn and Donald W. Crowe, University of Washington Press, 1988, was written to introduce anthropologists to the analysis of symmetry in patterns. Symmetry can often be used as a marker to help identify the decorative art of certain cultures. The book is filled with illustrations taken from many cultures, and has additional information on the analysis of two-color patterns, prevalent in many regions.
The Symmetries of ThingsThe Symmetries of Things, by John H. Conway, Heidi Burgiel, and Chaim Goodman-Strauss, A.K. Peters, 2008. This book gives an introduction to symmetries of two-dimensional patterns and three-dimensional solids (using coined names for the familiar isometries of translation, rotation, reflection, and glide-reflection). Filled with excellent illustrations, the book explains Conway’s orbifold notation for symmetry groups.
Tilings and Patterns

